Par Fournier Alain

À la recherche de l’étalon universel¹

Alain Fournier²

Résumé : Les mesures en usage avant le système métrique se rapportaient souvent à des parties du corps humain, moyen simple d’avoir des étalons « à portée de main ». Il existe ainsi une série remarquable allant de la paume à la coudée en croissant géométriquement selon le nombre d’or. Cette série comporte la « coudée royale », qui semble avoir servi pour l’Arche d’Alliance et pour le Temple de Salomon. En effet, en prenant cette coudée comme étalon, on découvre que notre mètre-étalon est égal au rayon des colonnes du Temple. Il se trace aussi aisément à partir du plan de l’Arche de Noé.Il existe donc un lien immédiat entre la coudée royale de 52,36 cm et le mètre. Le tableau de nombres harmoniques dit « série P », d’antique usage, comporte les anciennes mesures de longueur, évaluées en mètres.

Les Anciens n’ont pas dû éprouver d’énormes difficultés pour compter, mesurer, tracer, dessiner et réaliser.

Outre la description « chiffré » de certains éléments faite dans les textes anciens (chaldéens, égyptiens, la Bible, etc.), le moyen le plus simple pour dessiner ou tracer ce que l’on voulait réaliser fut certainement le dessin au sol – on l’utilisa jusqu’à la Renaissance et même après – grâce au compas avant la lettre que furent la corde et le bâton (canne, perche ou pige).

D’ailleurs, n’a-t-on pas représenté très souvent le Créateur du monde (voir les anciennes gravures) avec un compas en main ?

Pour peu que cette corde, ou cette canne, fût « dimensionnée » habilement et subtilement suivant des informations précises – et, pourquoi pas ?, « révélées » –, nos parents ne durent pas éprouver de difficultés majeures pour chiffrer, mesurer et construire harmonieusement. On connaît la « corde à nœuds » 3-4-5³ à 13 nœuds et douze intervalles égaux, ainsi que la canne et l’équerre des maîtres d’œuvre du Moyen Âge, canne proportionnée et subdivisée en reprenant les principales « mesures » utilisées par ces constructeurs.

Les Babyloniens utilisaient des tables de nombres permettant de construire des triangles rectangles : « La tablette Plimpton 322, qui se trouve actuellement dans les collections de l’université Columbia à New York, et datée de 1800 avant notre ère, présente un tableau de quinze triplets de tels nombres. Outre le 3-4-5 bien connu, on y trouve quatorze autres triangles, dont certains sont nettement plus complexes, comme le 65-72-97 ou encore le 1 679–2 400–2 929. À quelques petites coquilles près – erreurs de calcul ou de recopiage – les triangles de la tablette Plimpton sont parfaitement exacts : tous possèdent bien un angle droit⁴ ! »

La civilisation chinoise du I^er millénaire avant Jésus-Christ manifeste tout un savoir mathématique similaire à celui du Proche-Orient de l’époque. Le grand ouvrage intitulé Les Neuf chapitres sur l’art mathématique, compilé sous la dynastie Han, traite des triangles rectangles, à commencer par le 3-4-5⁵ .

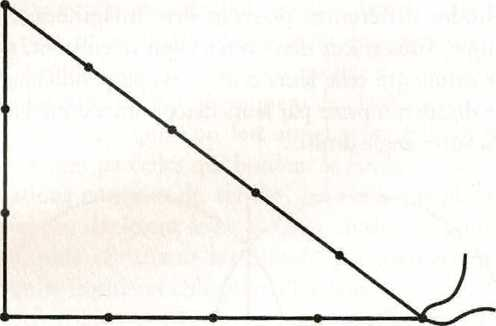
Fig. 1. La corde à 13 nœuds pouvant notamment servir d’équerre.

Divers auteurs ont entrepris des études systématiques sur ces mesures, tant les étalons furent nombreux et diversifiés au cours des âges. On s’accorde aujourd’hui sur une série-type dite, à juste titre, des initiés, tant par les auteurs profanes, voire agnostiques et même athées, que par les religieux (Mgr Ghika, Borissavlievitch, Charpentier, Fournier des Corats, Schwaller de Lubicz, Tourniac, Gouiran, Funck-Hellet, etc.). Les moines du Boscodon et de Sénanque ont merveilleusement synthétisé cela.

La série type des mesures est la suivante :

• La ligne⁶ 0,2247 cm
• La paume 7,64 cm
• Le palme⁷ 12,36 cm
• L’empan⁸ 20,00 cm
• Le pied 32,36 cm
• La coudée 52,36 cm

Il est évident que ces mesures vont différer d’un homme à l’autre, même si elles restent assez proches. Là n’est cependant pas la question.

Le but était d’obtenir une suite d’unités de mesure de référence permettant de respecter l’ordre et l’harmonie dans les réalisations. Le degré de perfection atteint par cette série est évident, on va le voir ; il faut admettre qu’elle supplante toutes les autres.

Remarquons tout d’abord que, du moins de la paume à la coudée, cette série est :

-une suite récurrente : chaque terme est égal à la somme des deux qui précèdent ;

-une suite géométrique : chaque terme est égal⁹ au produit de celui qui précède par Φ, le nombre d’or¹⁰, qui apparaît lui-même à la deuxième ligne du tableau, en colonne XII.

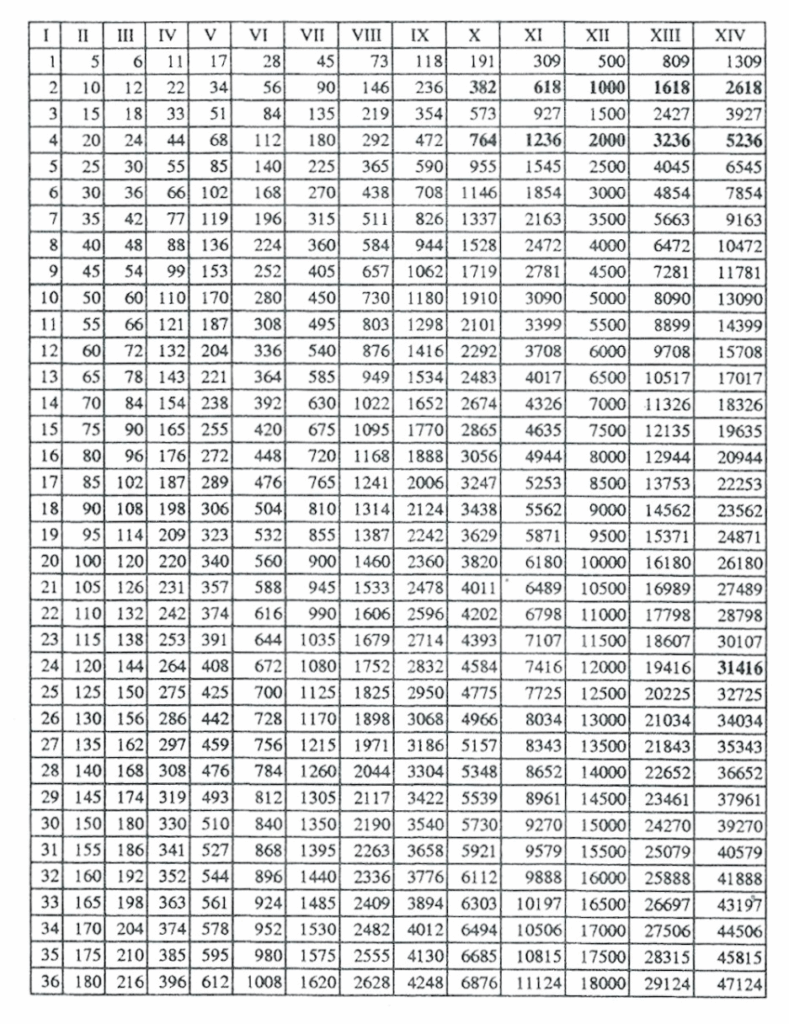
Ainsi, on la retrouve telle quelle dans la « série p », une sorte de « table de multiplication » connue et utilisée dans l’Antiquité (voir tableau en annexe) : tous ces nombres se retrouvent de la colonne X à la colonne XIV sur la quatrième ligne du tableau. Extrayons donc de ce tableau les colonnes X à XIV pour les lignes 2 et 4 :

	X	XI	XII	XIII	XIV
Ligne 2	382	618	1000	1618	2618
Soit :	1/Φ2	1/Φ	Φ0 = 1	Φ	Φ2
Ligne 4	764	1236	2000	3236	5236

On retrouve bien, sur la ligne 4, les dimensions des principales longueurs-étalon en usage depuis l’Antiquité, exprimées en centièmes de centimètres. Sur la ligne 2, multipliées par 1 000, les valeurs des différentes puissances du nombre d’or, Φ (Φ = 1,618). Le reste du tableau est une extrapolation qui permettait aux maîtres d’œuvre de connaître – sans avoir à les calculer – les dimensions harmonieuses à donner à leurs ouvrages.

L’énigme est alors la suivante. Ce tableau est d’abord un tableau numérique, établi selon une série mathématique très simple. Le départ de la série étant (en colonne II) le multiple de 5 correspondant au numéro de chaque ligne, les autres nombres de cette ligne en découlant par simple addition des deux termes antécédents. En même temps, ce tableau purement mathématique fait apparaître les mesures des principales unités de longueur, mais exprimées en centièmes de centimètres ! Or nous nous sommes persuadés que le mètre fut une noble invention du XVIII^e siècle…

En tout état de cause, cette série-étalon permet d’obtenir des valeurs métriques « normales » correspondant aux relevés sur le terrain avec, comme point de départ, un nombre entier de mesures élémentaires telles que les rapportent soit les textes, soit la Tradition.

Ces mesures-étalon sont inscrites dans la plupart des chefs-d’œuvre d’architecture de l’Antiquité, mais aussi du Moyen Âge, d’une partie de la Renaissance et de quelques rares « modernes », séquelle vraisemblable de la fameuse querelle dite des Anciens et des Modernes, qui opposa au XVII^e siècle, après la création de l’Académie royale de peinture et de sculpture à Paris (1648), les héritiers de l’architecte Philibert Delorme, François Blondel et le poète Nicolas Boileau, chefs de file des « Anciens », à Charles et Claude Perrault, ardents défenseurs et théoriciens des « Modernes ».

Après de multiples recherches, même encore inachevées, nous pouvons donc admettre que la valeur métrique de 0,5236 est bien celle de la « coudée royale » utilisée depuis la nuit des temps. Trop de relevés sont là pour le démontrer et trop de concordances en attestent le bien-fondé.

Mais d’où vient-elle ?

Vouloir rattacher cette mesure uniquement à une partie du corps humain semble quelque peu aléatoire, vu l’extrême diversité constatée sur les corps. Seule l’hypothèse d’un corps « premier » qui aurait donné une fois pour toutes cette « mesure » pourrait clore le débat. On aurait alors une sorte de « coudée d’Adam » ; mais jusqu’ici, rien n’a permis de la trouver explicitement.

Que cette mesure ait été reprise et utilisée par une partie de l’humanité se comprendrait. On pourrait même admettre que certains – par mimétisme ou par orgueil – aient pu vouloir changer cette mesure en adoptant une autre coudée (la leur), d’où la variété des étalons constatée, la coudée pouvant aller de 44 à 55 centimètres.

Par contre, le lien de la coudée royale de 52,36 cm avec le « mètre » est tel (et c’est la seule série dans ce cas) qu’il reste là un mystère à éclaircir. Du mètre, en effet, les Anciens ne parlent jamais, comme s’il avait été interdit de prononcer ce mot, un peu comme le Tétragramme YHWH. Il s’agit ici, bien entendu, d’une hypothèse.

Pour retrouver cela, le plus simple est de retourner aux sources en examinant quels rapports pouvaient relier la coudée royale (avec ses subdivisions) au mètre. Il est évident que les Anciens, par une géométrie simple, utilisaient ou déduisaient de quelques formes (cercles, carré, double carré) la plupart des mesures employées. Les textes égyptiens, chaldéens, sumériens, logiquement les plus anciens, s’ils comportent beaucoup d’indications mathématiques, astronomiques et symboliques, ne sont pas très diserts sur ce point précis. Il n’est dit nulle part que des bâtiments doivent être réalisés de telle ou telle façon et posséder telle ou telle mesure. On le constate, bien sûr ; mais tout s’arrête là.

En revanche, la Bible donne – parcimonieusement il est vrai – des indications intéressantes. Il s’agit surtout de la réalisation de l’Arche d’Alliance et des constructions dues au roi Salomon : le Temple et son environnement, la maison de Salomon lui-même et celle de son épouse « fille de Pharaon ». Un autre « édifice » est cité par la Bible avec des mesures précises : il s’agit de l’Arche de Noé.

La Bible nous dit que Dieu lui-même dicta aux constructeurs les « dimensions » (ainsi que les matériaux à utiliser) de ces réalisations (Gn 6, 15 sq. ; Ex 25, 10 sq. ; 1 R 6, 2 sq. ; 2 Ch 3, 3 sq.). Il y a aussi Ézéchiel 40, 3 et suivants, dont bizarrement peu d’auteurs reprennent les renseignements. Il y a pourtant là une mine à étudier.

Notons seulement qu’Ézéchiel rencontre un « homme muni d’une canne à mesurer de six coudées et d’une corde de lin ». Pour la canne de six coudées, Ézéchiel tient à préciser : « chaque coudée étant d’une coudée et un palme » (il s’agit donc cette fois des mesures courantes, soit la coudée de ±45 cm et le petit palme de 7-8 cm qui restera en usage chez les Romains, appelé paume dans la série ci-dessus). Ainsi, en additionnant la coudée ordinaire de 45 cm et le palme de 7,5 cm, soit 52,5 cm, on retombe quasiment sur la coudée royale de 52,36 cm, qui est donc la « vraie » coudée biblique, qui se dit אמה ʼamâh en hébreu.

Mentionnons enfin, avant d’entreprendre l’étude de l’arche de Noé, le travail exceptionnel réalisé par Charles Funck-Hellet¹¹ sur les fameuses colonnes (v. 1 R 7, 15) coulées par Hiram et sur le bassin appelé « la mer d’airain ».

À partir de ces deux éléments Funck-Hellet montre déjà que la coudée de 52,36 cm est liée au mètre et que, sans aucunes notions poussées de trigonométrie, il était possible aux maîtres d’œuvre de ce temps-là d’en avoir pleinement connaissance.

Des colonnes du Temple, il est dit, en effet, que « l’une était de dix-huit coudées de haut et un fil de douze coudées mesurait la circonférence de la seconde ».

Or, si douze coudées entourent une colonne cylindrique, sa douzième partie, soit une coudée, vaut l’arc sous-tendu par l’angle de 30° sur un cercle dont le rayon est alors de 1 mètre (suivant la formule arc = π r O/180 où r est le rayon et O l’angle en degrés). Plus simplement encore, la circonférence d’un cercle de rayon 1 m est 2π x 1, soit 6,2832 m, dont le douzième donne bien 0,5236 m, soit la valeur de la coudée royale¹².

Attardons-nous maintenant sur le plus ancien des édifices cotés, l’Arche de Noé. Si dans cette réalisation nous pouvions retrouver soit le mètre, soit un multiple parfait de ce mètre, nous pourrions dire que cette mesure, bien que jamais « dite », était connue.

L’Arche mesurait 50 coudées de large sur 300 de long et 30 coudées en hauteur (Gn 6, 15). On aurait donc, dans cette Arche construite pour que le rameau humain se perpétue, un plan de 300 x 50 coudées.

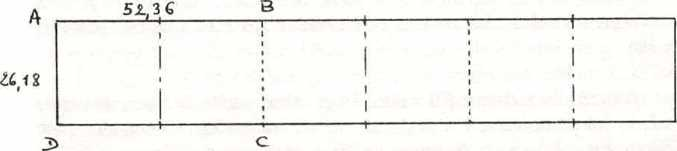
Fig. A : Plan horizontal de l’Arche mesurée en mètres.

Ce plan, selon le partitionnement toujours utilisé dans l’Antiquité, se découpe ainsi (voir Fig. A) :

1/ soit en 6 modules carrés de 50 x50 coudées : en valeur métrique, avec la coudée de 0,5236 m, mesurant donc chacun 26,18 x 26,18 mètres carrés.

Ce qui peut donner une « modulation » de 5 x 5 coudées pour la répartition des pièces (puisque la Bible dit que Noé fit des cellules), soit des espaces de 2,618 x 2,618 m (6,854 m²), soit de 5 x 10 coudées engendrant des espaces de 2,618 x 5,236 m (double-carré de 13,707 m²), éventuellement de 10 coudées au carré (27,415 m²), tous espaces pouvant correspondre à des cabines de bateau.

On peut aller plus loin par modules de 5 coudées. Une première particularité est que 26,18 m est exactement la valeur de Φ² x 10 mètres !

2/ soit 3 modules en doubles-carrés de 50 x 100 coudées, mesurant donc chacun 26,18 m x 52,36 m. Donc 3 doubles carrés ABCD, dont les côtés sont égaux aux arcs de 30° (pour 52,36 m) et 15° (pour 26,18 m) sur un cercle de 100 m de rayon.

Si l’on isole un de ces doubles carrés ABCD et que l’on y place le tracé simple donnant les proportions de base, on trouve (figure B) une diagonale AC valant √5, traversant le cercle de centre O dont le diamètre vaut 50 coudées ou 26,18 m (pour rappel 26,18 = Φ² x 10).

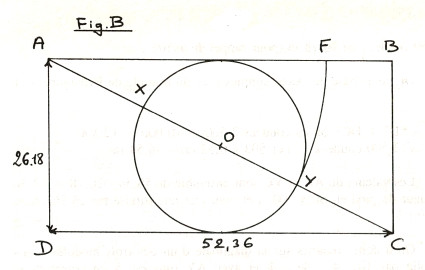
Fig. B : Tracés divers dans un double-carré de l’Arche.

Sur la base de calculs simples tirés du triangle de Pythagore, on a ici :

AC² = AD² + DC² ou en coudées 2 500 + 10 000 = 12 500

AC = √12 500 coudées = 111,803 coudées x 0,5236 = 58,54 m

Les valeurs de AX et YC sont donc ensemble de :

58,54 – 26,18 = 32,36 m (valeur du pied en mètres x 100 !) et pour chacune (divisée par 2) 16,18 ou Φ x 10 !

Avec les segments AX, XY et YC, on remarque donc, répartis sur la diagonale d’un des trois modules de l’Arche (mais multipliés par 10) : Φ – Φ² – Φ ; et avec AY qui vaut ici 26,18 + 16,18 = 42,36, soit Φ³ (toujours multiplié par 10) ! Si la base AD mesure 1 et donc 2 pour AB, alors AY est égal à Φ : toujours l’harmonie des proportions assurée par le nombre d’or.

À ce stade, si je rabats AY sur AB (cf. Fig. B), j’obtiens le point F qui me donne un rectangle d’or AFF’D avec comme côtés 42,36 et 26,18 m (Fig. C).

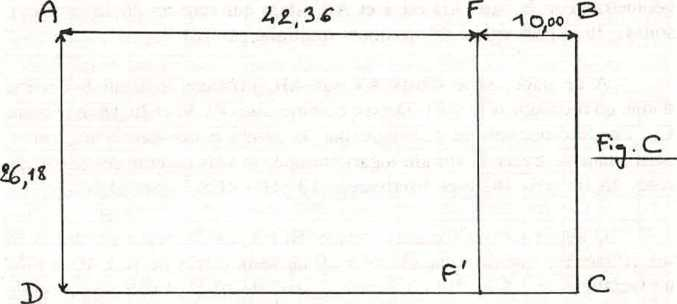
Fig. C : Le « reste », mesuré en mètres, dans l’Arche de Noé.

En décomposant ce rectangle par le principe des carrés tournants, permettant de tracer la spirale dite logarithmique (ou spirale d’or), je vais obtenir des carrés de côtés 26,18, puis 16,18 et finalement 10 mètres (Fig. D).

D’autres part le rectangle restant BFF’C est un rectangle de 26,18 par 10 mètres, soit un rectangle Φ² x 10 ou deux carrés de 10 x 10 m plus un rectangle de l/ Φ (x 10), soit encore 1 carré de 10 x 10 plus un rectangle de longueur Φ (x 10).

À partir du segment FB valant 10 m, il est facile de tracer le cercle du même rayon donnant à l’angle de 30 la valeur de 10 coudées (soit 5,236 m) et, par subdivision du rayon en 10 parties égales, d’obtenir à la fois et le mètre et la coudée sur la même figure (Fig. E).

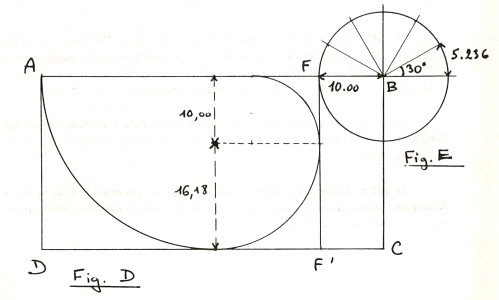
Fig. D :La spirale logarithmique.

Fig. E : Le cercle de rayon 10 m.

Sans changer d’échelle, on pourrait encore obtenir la coudée en prenant l’arc sous-tendu par un angle de 3° (subdivision par 10 de l’arc sous-tendu par le rayon de 10 m. et l’angle de 30°). Tout cela suffit à démonter l’importance des principes d’harmonie utilisés par les constructeurs depuis la plus haute antiquité.

Annexe. Tableau de la « série P »

---

1 Une première version de cet article avait été publiée dans Science et Foi n°36, 2^e trimestre 1995, p. 23, ici reprise, remaniée et complétée par nous.

2 Architecte belge (1942-2009), il fut Président du CESHE.

3 Cette corde à 13 nœuds équidistants permet notamment de tracer un angle droit : angle au sommet du triangle rectangle mesurant 5 unités à l’hypoténuse et 3 et 4 unités sur les côtés.

4 Mickaël LAUNAY, Le Grand Roman des maths de la Préhistoire à nos jours, Paris, Flammarion, 2016, p. 44.

5 Ibidem, p. 45.

6 La ligne représente l’épaisseur d’un grain d’orge.

7 Le palme est la mesure qui va de l’extrémité du petit doigt à celle de l’index (doigts écartés).

8 L’empan va de l’extrémité du petit doigt à celle du pouce (doigts écartés).

9 Ndlr. Ou presque égal, lorsque ces nombres entiers sont trop petits pour donner une approximation assez fine.

10 Φ est égal à la moitié de 1 + 5, soit 1,618. C’est la longueur du grand côté d’un « rectangle parfait » dont le petit côté mesure 1. Si l’on retire de ce rectangle le carré construit sur son petit côté, le « reste » constitue à nouveau un rectangle parfait et cette propriété sert à tracer une spirale avec le compas ; cf. Fig. D.

11 Ch. FUNK-HELLET, La Bible et la Grande Pyramide. Témoignages authentiques du mètre et de π, Paris, Éd. Vincent, Réal & Cie, 1956.

12 Ndlr. En clair, ceci veut dire (cf. Fig. E) que notre mètre-étalon est le rayon des colonnes du Temple de Salomon. On comprend que la maçonnerie opérative ait pu en transmettre la valeur et que la maçonnerie spéculative l’ait imposée à l’humanité à la faveur de la Révolution.