Partager la publication "Le système terre-lune et les forces de marée"
Par le Dr Eric Ballaux
Résumé : Jusqu’à présent on considérait comme impossible de prédire la force des marées par le seul calcul astronomique. C’est une méthode empirique qui est utilisée depuis des siècles en navigation pour prévoir les marées et l’accès aux ports. L’auteur propose ici une théorie gravimétrique et mécanique simple et, pour la valider, calcule la force de marée qui devrait être observée lors de l’éclipse solaire du 11 août 1999.
Sous l’influence du soleil et de la lune, la pesanteur à la surface de la terre subit de petites variations, qui sont la cause des marées. Ces variations peuvent être mesurée avec une grande précision au moyen de gravimètres.
Actuellement, la prévision de la force de marée ne se fait que sur une base empirique. Les enregistrement gravimétriques sur de longues périodes sont analysés puis décomposés en centaines d’ondes, en fonction de différents paramètres astronomiques. Au moyen de ces données, on peut calculer et prévoir avec une bonne précision la force de marée à un endroit donné. Cette méthode est purement déductive et peut être appliquée sans aucune base théorique. Une méthode déductive comparable est employée depuis des siècles en navigation pour prévoir les marées et l’accès aux ports.
1. Le centre de masse du système terre-lune
Le centre de masse commun du système terre-lune (CMC), situé à 4.671 km du centre de masse de la terre en direction de la lune, suit l’orbite du système terre-lune autour du soleil. Le déplacement excentrique de la terre par rapport au CMC est confirmé par l’aberration mensuelle et par des mesures Doppler avec des satellites artificiels. Ces observations ne donnent aucun renseignement sur le centre de rotation commun réel de la lune et de la terre, qui peut être différent du CMC.
2. Notre hypothèse : le centre de rotation commun du système terre-lune.
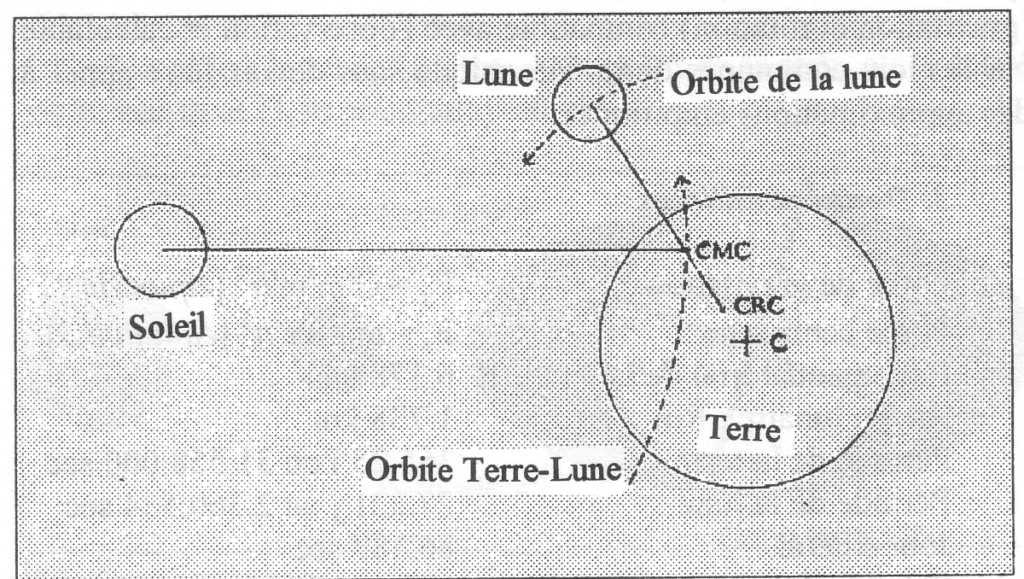
Fig.1. Le système terre-lune
Une partie des astronomes nie tout effet de marée d’origine centrifuge. Une autre partie des astronomes tient compte d’un effet centrifuge, causé par la rotation supposée de la terre autour du centre de masse du système terre lune, situé autour de 4.671 km du centre de la terre en direction de la lune. Mais cet effet n’est jamais calculé. Et pour cause : l’effet de marée généré par la rotation de la terre autour du CMC devrait être asymétrique et au moins dix fois plus important que la force de marée mesurée.
Selon notre hypothèse, le centre de rotation commun du système terre-lune autour du soleil (CRC), distinct du centre de masse commun (CMC), est situé entre 141 et 163 km du centre de la terre, en direction de la lune.
On constate en effet que la force de marée est symétrique aux deux côtés opposés de la terre. Cette symétrie n’est possible que si l’effet gravitationnel de marée de la lune (nécessairement asymétrique par rapport à l’axe de la rotation terre-lune) est compensé par un effet centrifuge.
L’hypothèse d’un centre de rotation commun (CRC) beaucoup plus proche de la terre que le centre de masse du système terre-lune (CMC), donne une force de marée résultante (gravitation et rotation) compatible avec l’observation et calculable par les lois communes de la Mécanique sans devoir faire appel à des approximations empiriques.
3. Données utilisées
Force de gravitation Fg = G.m.m’/r2 [équation 1]
Force centrifuge Fc = m.r.4(2/t2 [équation 2]
Rayon équatorial de la terre : R 6.378 km
Rayon lunaire : Rm 1.738 km
Période de la terre : 365,25 j ou 31.558.000 sec
Période de la lune : 27,321 j ou 2.360.534 sec
Jour sidéral 86.187 sec
Soleil :
– périhélie 147.100.000 km
– distance moyenne (inter) 149.598.000 km (Dms)
– aphélie 152.598.000 km
Lune :
– périgée 356.400 km
– distance moyenne (inter) 383.200 km (Dml)
– apogée 410.000 km
Masse-lune / Masse-terre 0,0123
Masse-soleil / Masse-terre 332.946
La constante de gravitation (G) n’est pas utilisée car elle disparaît, par simplification, dans tous les calculs.
4. L’action du soleil
4.1 Orbite de la terre autour du soleil. Attraction1.
Soit C le centre de la terre, As le point de la terre où le soleil est au zénith et Os le point antipode de As.
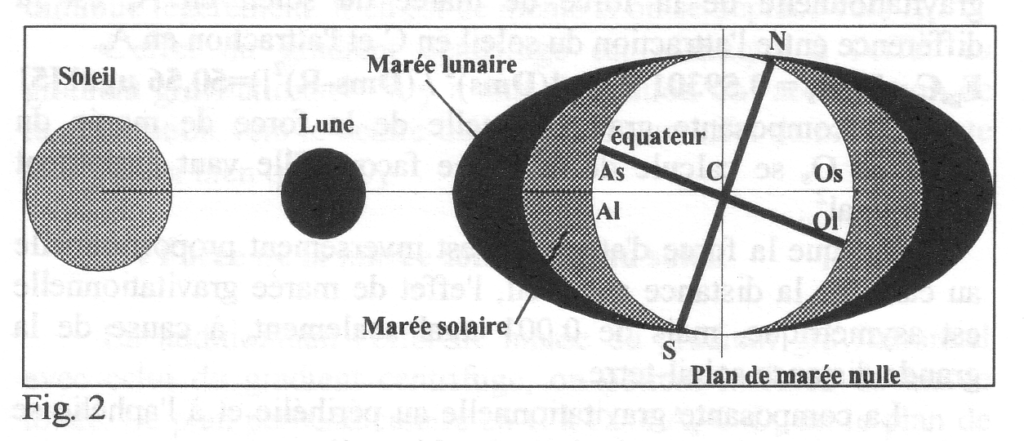
L’exentricité de l’orbite de la terre autour du soleil étant faible, nous allons considérer cette orbite comme circulaire. Nous pouvons calculer maintenant la force centrifuge de la terre à la distance moyenne soleil-terre (FcsC-inter) en appliquant l’équation 2 (Fc = mr (2), soit:
FcsC-inter=(149.598.000km)4(2/(31.558.000sec)2=0,59301cm/s2 par unité de masse [équation 4].
Nous allons également supposer que, au point C, l’attraction est égale à la force centrifuge à chaque position sur l’orbite terrestre. L’attraction et la force centrifuge au périhélie et à l’aphélie peuvent être déduites de FcsC-inter au moyen de l’équation 1 et sont données dans le tableau 1
4.2 Composante gravitationnelle de la force de marée du soleil
L’attraction du soleil est plus grande en As qu’en C, à cause de la différence de distance par rapport au soleil (fig.2). L’attraction est plus petite en Os qu’en C. La composante gravitationnelle de la force de marée du soleil en As est la différence entre l’attraction du soleil en C et l’attraction en As.
FgsC – FgsAs = 0,59301 x (1- [(Dms)2 / (Dms-R)2])=50,56 µgal [5]
La composante gravitationnelle de la force de marée du soleil en Os se calcule de la même façon. Elle vaut également 50,56 µgal2.
Puisque la force d’attraction est inversement proportionnelle au carré de la distance au soleil, l’effet de marée gravitationnelle est asymétrique, mais de 0,001 µgal seulement, à cause de la grande distance soleil-terre.
La composante gravitationnelle au périhélie et à l’aphélie se calcule par la même méthode (voir tableau 1).
Quand on se déplace de C vers As, l’attraction du soleil augmente, donc la pesanteur vers C diminue : il en résulte une légère diminution de l’accélération de la gravitation en As, un effet de marée haute. Quand on se déplace de C vers Os, l’attraction vers le soleil diminue, donc la pesanteur totale diminue : il en résulte également un effet de marée haute en Os. L’attraction d’un corps astronomique (le soleil, la lune, …) produit ainsi un gradient gravitationnel de As vers Os et une force de marée aux deux côtés de la terre. C’est pourquoi il y a 2 marées par jour.
4.3 Composante centrifuge de la force de marée du soleil
La force centrifuge autour du soleil est proportionnelle à la distance. Elle est donc plus petite en As qu’en C et plus grande en Os qu’en C. La différence entre la force centrifuge en C (FcsC) et en As (FcsAs) est la composante centrifuge de la force de marée du soleil en As.
FcsC – FcsAs = 0,59301x (1-[(Dms – R) / Dms]) = 25.26 µgal [6]
La composante centrifuge en Os est également 25.26 µgal. La composante centrifuge en As et Os au périhélie et à l’aphélie est calculée par la même méthode (Tableau 1).
Si on se déplace de C (ou du plan de force de marée nulle) vers Os, l’attraction gravitationnelle vers le centre de la terre diminue légèrement. Il en est de même si on se déplace vers As.
L’effet du gradient centrifuge est identique à l’effet du gradient gravitationnel : il y a une diminution de l’accélération de la gravitation vers le centre de la terre ou un effet de marée haute en As aussi bien qu’en Os.
4.4 Force de la marée totale due au soleil
En additionnant l’effet de marée du gradient gravitationnel avec celui du gradient centrifuge, on obtient la force de marée totale. Le plan perpendiculaire en C à l’axe As-C-Os est le plan de « force de marée nulle » du soleil.
Tableau 1 : La force de marée due au soleil Fm.As (Os)
| Distance terre-soleil | Périhélie 147.100.000 | Inter 149.598.000 | Aphélie 152.100.000 |
| Attraction en C (gal) | 0,61332 | 0,59301 | 0,57366 |
| Comp.gravitat. (µgal) | 53,0 | 50,56 | 48,05 |
| Comp. centrifuge (µgal) | 26,5 | 25,26 | 24,05 |
| Total (µgal) | 79,5 | 75,82 | 72,10 |
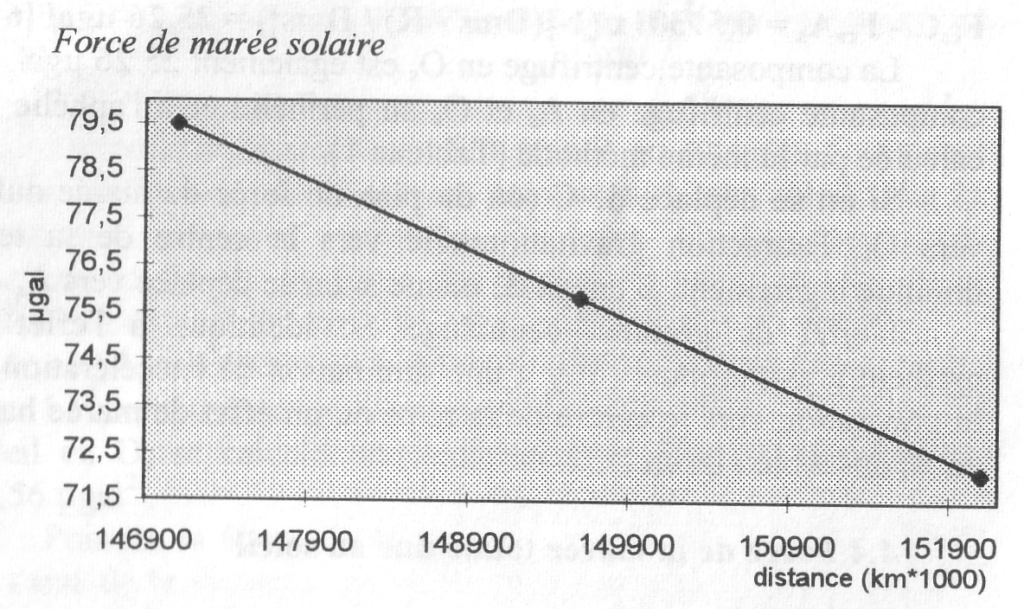
Le calcul de la composante verticale de la force de marée du soleil en un point P de la surface de la terre, nécessite une double correction ( P-C-As ou P-C-Os) :
1. pour le calcul de la magnitude de la force de marée locale, qui dépend de la distance P-« plan de force de marée nulle » et dont le vecteur est parallèle à l’axe As-Os ;
2. pour calculer la composante verticale de la force ainsi calculée.
En appliquant ces 2 corrections, on obtient pour la force de marée du soleil en un point P de la surface terrestre :
Fmv.P =Fm.As (Os) x cos2 P-C-As (Os)
La composante horizontale en direction de l’axe soleil-terre (centres de masse) est elle :
Fmh.P = Fm. As (Os) x cos P-C-As (Os) x sin P-C-As (Os).
5. L’action de la Lune
5.1. Notre modèle théorique du système terre-lune
La lune et la terre sont en orbite elliptique autour d’un centre commun de rotation (CRC). Ces deux ellipses ont le même foyer (CRC) et la même période. Les positions apo, péri, et inter des deux orbites sont parcourues de façon synchrone.
Le centre de rotation du système terre-lune est mobile, localisé entre 141 km et 163 km du centre de la terre en direction de la lune.
La force de marée de la lune a deux composantes : (1) la composante gravitationnelle lune-sur-terre et (2) la composante centrifuge, due à la rotation de la terre autour du centre de rotation avec la lune.
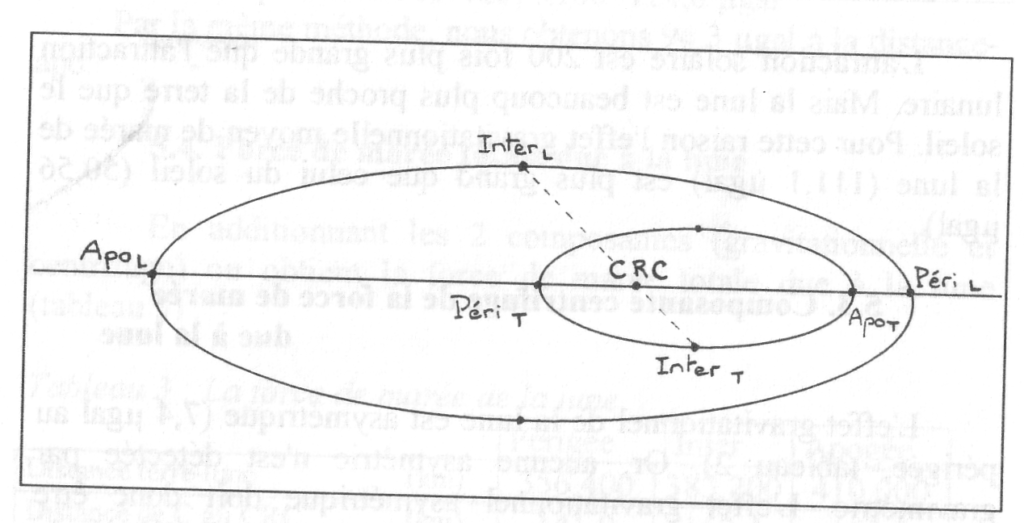
Fig. 3 Le système terre-lune (t=terre l=lune)
5.2. Composante gravitationnelle de la force de marée due à la lune
La figure 2 montre que les effets gravitationnels calculés au paragraphe 4.2 pour le soleil se transposent à la lune en les corrigeant par le rapport de masse lune/soleil et le carré du rapport des distances.
| Périgée | Inter | Apogée | |||||
| Distance en km | 356.400 | 383.200 | 410.000 | ||||
| FglC en gal | 0,0038598 | 0,0033388 | 0,0029165 | ||||
| Gradient (A1èC) | (CèO1) | 141,9 | 134,5 | 113,9 | 108,4 | 92,9 | 88,6 |
| F. marée en A1 ou en O1 (µgal) | 138,2 | 111,1 | 90,7 | ||||
Tableau 2 : L’effet gravitationnel lune-sur-terre
L’attraction solaire est 200 fois plus grande que l’attraction lunaire. Mais la lune est beaucoup plus proche de la terre que le soleil. Pour cette raison l’effet gravitationnelle moyen de marée de la lune (111,1 µgal) est plus grand que celui du soleil (50,56 µgal).
5.3. Composante centrifuge de la force de marée due à la lune
L’effet gravitationnel de la lune est asymétrique (7,4 µgal au périgée, tableau 2). Or, aucune asymétrie n’est détectée par gravimétrie. L’effet gravitationnel asymétrique doit donc être compensé par la force centrifuge, générée par la rotation de la terre autour du centre de rotation commun avec la lune (CRC). La compensation est excellente quand la valeur du gradient centrifuge est proche de la valeur du gradient gravitationnel. La valeur du gradient centrifuge à la distance-inter est estimée à 216 µgal. Tous les calculs faits à partir de cette valeur sont confirmés par gravimétrie. Une petite correction de la valeur adoptée serait possible, valeur à déterminer par gravimétrie. En renversant l’équation 2 on constate qu’un gradient de 216 µgal correspond à une rotation excentrique de la terre de : r = Fc.t2 / 4π2
Soit : [(0,000108) x (2.360.534)2] /4 π 2 = 152,4 km
A cause de la forme symétrique de l’orbite de la terre et de la lune, l’axe-péri sur l’orbite de la terre mesure 141,7 km et l’axe-apo mesure 163 km.
Comme nous l’avons fait pour l’orbite de la terre autour du soleil, nous supposons que l’attraction égale la force centrifuge en chaque point de l’orbite de la lune autour du CRC. Considérons les orbites de la lune et de la terre autour du CRC (fig.3). Entre deux positions symétriques de l’orbite de la lune et de l’orbite de la terre, la force centrifuge change dans les mêmes proportions. Nous pouvons donc calculer un changement de la force centrifuge dans l’orbite de la terre en la comparant au changement correspondant dans l’orbite de la lune. Pour cette raison, la force centrifuge générée par la rotation excentrique de la terre à la distance-péri devient :
[383.200/356.400]2x108=124,8 µgal
Par la même méthode, nous obtenons 94,3 µgal à la distance-apo.
5.4. Force de marée totale due à la lune .
En additionnant les 2 composantes (gravitationnelle et centrifuge) on obtient la force de marée totale due à la lune (tableau 3) :
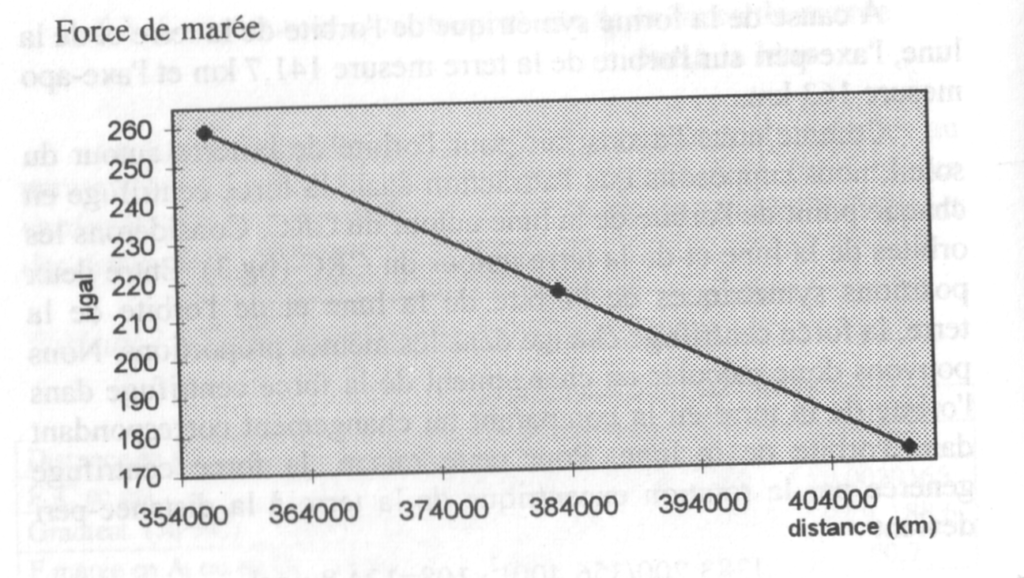
Tableau 3 : La force de marée de la lune
| Périgée | Inter | Apogée | |
| Distance terre-lune (km) | 356.400 | 383.200 | 410.000 |
| Distance de C au CRC (km) | 141,0 | 152,4 | 163,0 |
| Composante gravitationnelle (µgal) | 138,2 | 111,1 | 90,6 |
| Composante centrifuge (µgal) | 124,8 | 108,0 | 94,3 |
| Total (µgal) | 263,0 | 219,1 | 184,9 |
Le plan perpendiculaire en C à l’axe Al-C-Ol est le plan « force de marée nulle » de la lune (voir figure 2).
La force de marée de la lune en un point P de la surface terrestre se calcule par correction de la force de marée en Al (ou Ol) : Fl.P= Fl.Al x cos2 P-C-Al
6. La force de marée combinée du soleil et de la lune
L’effet total de la force de marée du soleil et de la lune dépend de l’angle soleil-terre-lune. Quand il y a alignement soleil – lune – terre, le maximum théorique, soleil + lune peut atteindre 79,5 + 263,0 = 342,5 µgal. Quand la lune et le soleil sont en quadrature, le minimum peut atteindre 184,9 – 79,5 = 105,4 µgal (de – 79,5 à – 184,9 µgal par rapport à la valeur « force de marée nulle »). Ces situations extrêmes peuvent ne pas se rencontrer en réalité.
Entre les deux, en chaque point de la surface terrestre, et pour chaque configuration astronomique, on peut calculer la force de marée combinée en additionnant les 2 forces de marée.
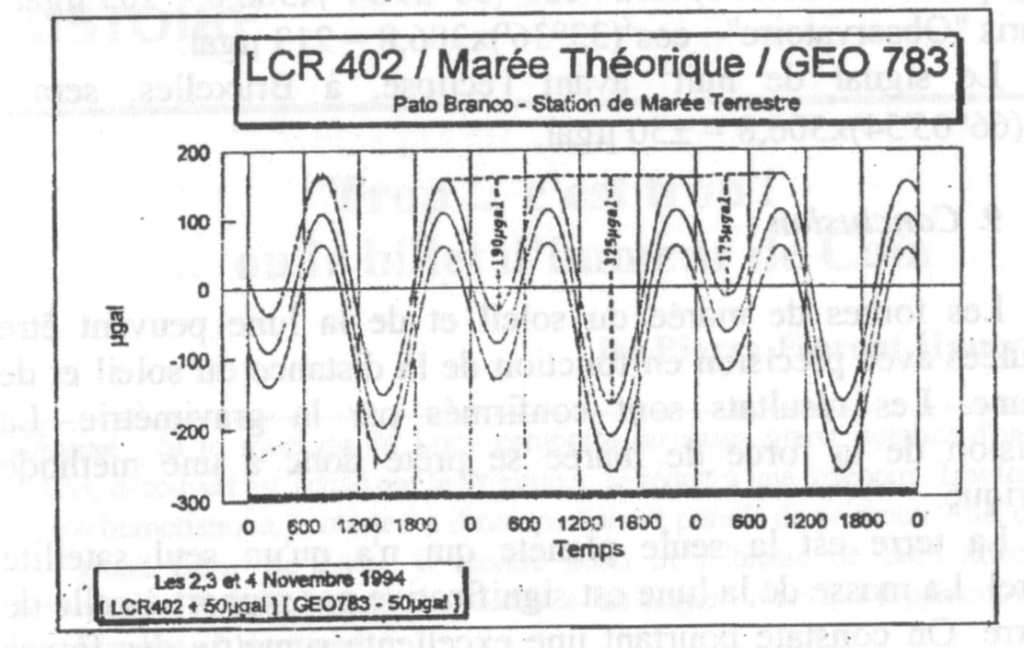
Ainsi lors de l’éclipse solaire observée à Pato Branco (Brésil) le 3 novembre 1994 à 13h, notre calcul donne une composante verticale de 326,3 µgal, alors que la valeur observée fut de 325 µgal, donc très proche de la valeur théorique.
Tableau 4 : Variation de la pesanteur à Pato Branco (3/11/94)
7. Autres effets gravitationnels
Nous avons calculé d’autres effets possibles sur les marées. Ils sont tous beaucoup plus faibles et peuvent être négligés pour le moment. L’effet gravitationnel dû aux planètes est au plus de 0,0054 µgal pour Vénus et 0,0006 µgal pour Jupiter.
8. L’éclipse solaire du 11 août 1999.
Les calculs étant très faciles lors d’une éclipse, du fait de l’alignement, nous avons calculé la force théorique de marée, le 11 août à midi, afin de tester la valeur prédictive de notre hypothèse :
Calcul de la force de marée pendant l’éclipse de 1999 :
Soleil : distance 151.630.000 km ; Lune: distance 373.215 km
Marée solaire : 48,5 gravit. + 24,2 centrif. = 72,7 µgal
Marée lunaire : 120,3 gravit. + 113,8 centrif. = 234,1 µgal
Marée totale : 306,8 µgal
Le maximum de la force de marée pendant l’éclipse solaire du 11 août 1999, 306,8 µgal, peut être mesuré à 15°20′ N – 10°0 (midi local) ou à 15°20′ S – 170°E (minuit local).
La force de marée à Bruxelles « Observatoire Royal de Belgique » (midi solaire) sera : cos2 (35°29’54 »)x306,8 = 203 µgal ; à Paris « Observatoire » : cos2(33°36′)x306,8 = 213 µgal.
Le signal de nuit3 avant l’éclipse, à Bruxelles, sera : cos2(66°05’54)x306,8 = (50 µgal.
9. Conclusion
Les forces de marée du soleil et de la lune peuvent être calculées avec précision en fonction de la distance du soleil et de la lune. Les résultats sont confirmés par la gravimétrie. La prévision de la force de marée se prête donc à une méthode théorique.
La terre est la seule planète qui n’a qu’un seul satellite naturel. La masse de la lune est significative par rapport à celle de la terre. On constate pourtant une excellente symétrie des forces de marée aux deux côtés opposés de la terre.
Un second satellite, – même petit, mais plus proche,- perturberait le mécanisme parfaitement équilibré des marées.
Le présent article, dont les lecteurs auront compris toute l’importance théorique et pratique, est extrait d’une plaquette plus détaillée diffusée par l’auteur : Eric Ballaux Steenweg Diest, 65, B-3271 Scherpenheuvel-Zichem (Belgique). E-mail : eric.ballaux.@planetinternet.be
1 Ndlr. Nous ne discuterons pas ici la question de savoir si cette « attraction » apparente résulte d’une activité inhérente aux masses en présence (comme Newton se gardait bien de l’affirmer) ou d’un effet de répulsion par la matière cosmique (gravitation, théorie de Lesage)… L’éclipse du 11 août apportera peut-être un éclairage utile sur ce point.
2 1 gal = 1cm/s2. 1 µgal = 10-6 gal
