L’architecture des cristaux

Par Albert de Lapparent

Regard sur la création

« Car, depuis la création du monde, les perfections invisibles de Dieu, sa puissance éternelle et sa divinité, se voient comme à l’œil quand on Le considère dans ses ouvrages. » (Romains, 1 : 20)

L’architecture des cristaux¹

Albert de Lapparent²

Résumé : Les si curieuses associations que forment les cristaux ne peuvent s’expliquer que par le besoin de conquérir, à l’aide d’une symétrie plus élevée, une résistance plus complète à l’égard des causes extérieures de destruction ; phénomène téléologique au premier chef, puisqu’il se réalise en des objets chez lesquels il n’est permis d’admettre ni instinct, ni calcul, ni tâtonnements, ni dispositions transmises par héritage. C’est donc une preuve manifeste de l’Intelligence créatrice que nous donnent les cristaux de staurotide, de gypse, de christianite, de diamant, et bien d’autres encore.

A travers les phénomènes de la nature, éclate de manière constante l’application du principe de la moindre action, si conforme à l’idée que nous pouvons nous faire d’une Suprême Sagesse ordonnatrice.

Le principe prévaut sans conteste en Mécanique où on le formule de la manière suivante : une particule matérielle en mouvement, soustraite à l’influence de toute force, mais assujettie à demeurer sur une surface déterminée, prendra toujours, pour se rendre d’un point à un autre, une ligne géodésique de la surface, c’est-à-dire le chemin le plus court entre les deux points.

Certains esprits ne dissimulent pas que cet énoncé les choque, parce qu’il paraît donner à penser que la particule « semble connaître le point où on veut la mener, prévoir le temps qu’elle mettra à l’atteindre en suivant tel ou tel chemin, et choisir ensuite le plus convenable. »³

Pour nous, qui ne saurions être soupçonnés d’attribuer à la particule un tel discernement, il nous plaît, au contraire, de mieux apercevoir à travers cet énoncé la marque de l’infaillible sagesse avec laquelle toutes choses ont été combinées.

Dans le domaine de la physique, il n’est pas de chapitre où la règle de la moindre action se manifeste avec plus d’éclat que celui de la réflexion et de la réfraction de la lumière. On sait que, quand un rayon lumineux tombe obliquement sur une surface réfléchissante, il est renvoyé de telle sorte que le rayon incident et le rayon réfléchi, tous deux contenus dans un plan perpendiculaire à la surface, soient inclinés du même angle sur le miroir.

Or si l’on pose ce problème : étant donnés deux points quelconques hors d’un plan, quelle est la condition pour que la lumière, partie de l’un, arrive à l’autre par le chemin le plus court, après avoir, au préalable, touché le plan ? On trouvera immédiatement que ce chemin doit être une ligne brisée, suivant exactement le parcours indiqué par la loi expérimentale, dite loi de Descartes. Que la lumière soit un projectile, comme le croyait Newton, ou un ébranlement se propageant dans l’éther, suivant la théorie des vibrations, ou encore un phénomène électro-magnétique, peu importe ; c’est toujours une question de minimum : minimum de chemin parcouru ou minimum d’énergie dépensée ; en un mot, application de la règle de moindre action.

Il en est de même lorsque la lumière, après avoir cheminé dans le vide ou dans l’air, rencontre un corps transparent, tel qu’une lame de verre ou de cristal. Pour aller d’un point, situé dans le premier milieu, à un autre, pris dans le second, la lumière pourrait suivre la ligne droite qui les joint. Mais, comme elle se propage beaucoup moins vite dans le second milieu, il y a intérêt à ce que son parcours y soit réduit. Le calcul indique que, pour réaliser le maximum de vitesse, il faut qu’il y ait, entre ce qu’on appelle les sinus des angles d’incidence et de réfraction, un rapport constant, précisément égal au rapport des vitesses dans les deux milieux ; c’est exactement ce que vérifie l’expérience.

Ainsi les deux lois fondamentales de la propagation de la lumière auraient pu être déterminées d’avance, sans aucun recours à l’observation, par cette seule condition qu’il y eût, dans toute hypothèse, le minimum de travail dépensé.

De tous les exemples qu’on peut invoquer pour montrer la généralité du principe de la moindre action, il en est peu dont la signification soit plus claire que celle des arrangements si souvent réalisés par les cristaux. C’est d’abord la fréquence bien constatée des formes les plus simples, qui justement correspondent au maximum de cohésion, c’est-à-dire de stabilité, pour les faces ainsi produites. Ainsi, dans le système cubique, le cube, l’octaèdre, le dodécaèdre à faces losanges l’emportent incomparablement sur les formes plus compliquées. De même, dans tous les systèmes, les combinaisons de clivages ou de propriétés optiques correspondent presque toujours aux solutions les plus simples, parmi celles que la symétrie autoriserait à prévoir.

Mais ce qui est surtout frappant, c’est ce qu’on pourrait appeler l’ingéniosité déployée, par les assemblages de cristaux, pour réaliser une stabilité supérieure à celle que leur système semblait autoriser. Tel cristal, comme la staurotide ou croisette de Bretagne, qui devrait se présenter sous la forme d’un prisme allongé, à base de losange, a coutume d’associer deux de ces prismes à angle droit, de manière à former une croix presque parfaite, qui donne à l’ensemble une même résistance suivant deux directions rectangulaires.

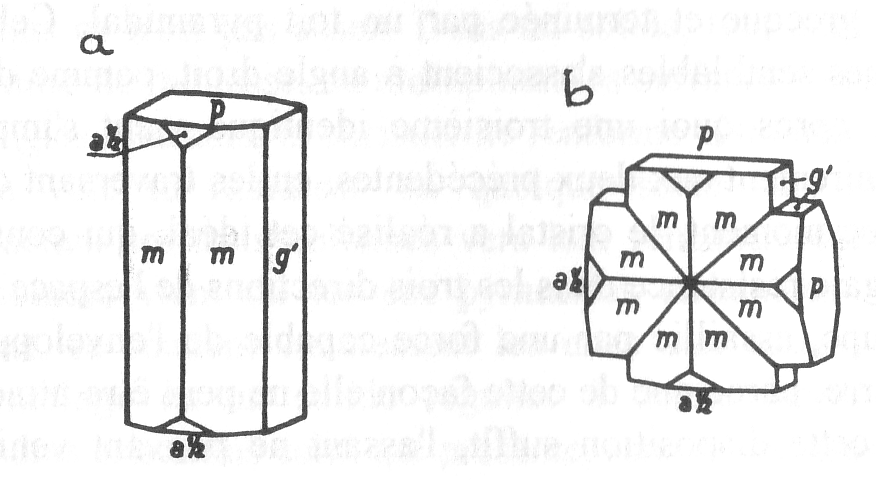
Fig. 1. Staurotide. a) prisme simple, b) cristal maclé en croix.

Tel autre, comme le gypse ou sulfate de chaux, qui n’a qu’un seul plan de symétrie, se macle, suivant l’expression usitée, de manière que l’ensemble arrive à en posséder trois.

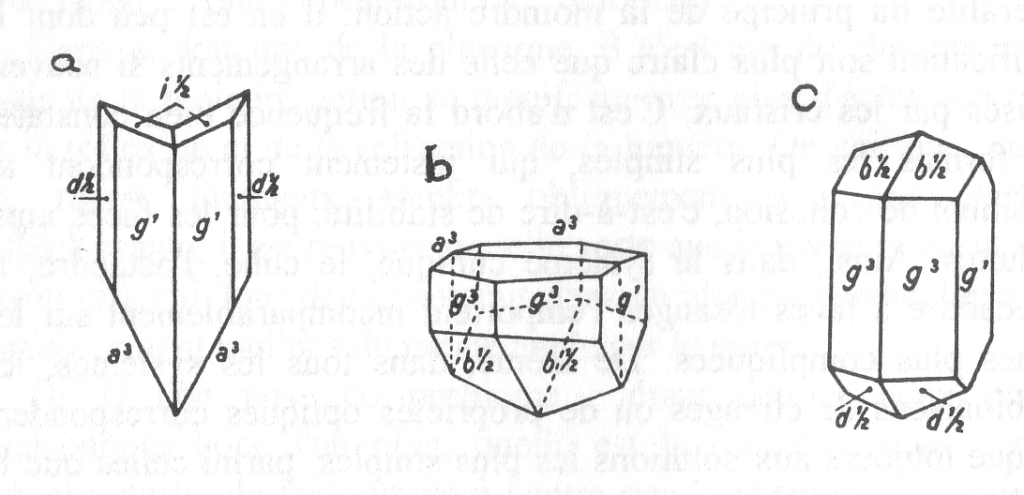
Fig. 2. Gypse. a) macle en fer de lance, b) macle à 2 plans de symétrie, c) macle à 3 plans de symétrie.

Un exemple encore plus instructif est celui de la christianite⁴, qu’on rencontre dans les vacuoles de quelques laves. Cette espèce, qui ne possède qu’une symétrie peu élevée, commence par grouper plusieurs individus en une colonne prismatique ayant la section d’une croix grecque et terminée par un toit pyramidal. Cela fait, deux colonnes semblables s’associent à angle droit, comme dans la staurotide ; après quoi une troisième identique vient s’implanter perpendiculairement aux deux précédentes, en les traversant de part en part. A ce moment, le cristal a réalisé cet idéal, qui consiste à offrir une égale résistance dans les trois directions de l’espace.

Une troupe, assaillie par une force capable de l’envelopper, se forme en carré, parce que de cette façon elle ne peut être attaquée à revers ; et cette disposition suffit, l’assaut ne pouvant venir d’en haut.

Obligée de prévoir d’autres attaques, la christianite y pourvoit par sa disposition en double croix grecque, semblable à l’instrument que les couvreurs ont l’habitude de suspendre à une corde afin d’avertir qu’une toiture est en réparation

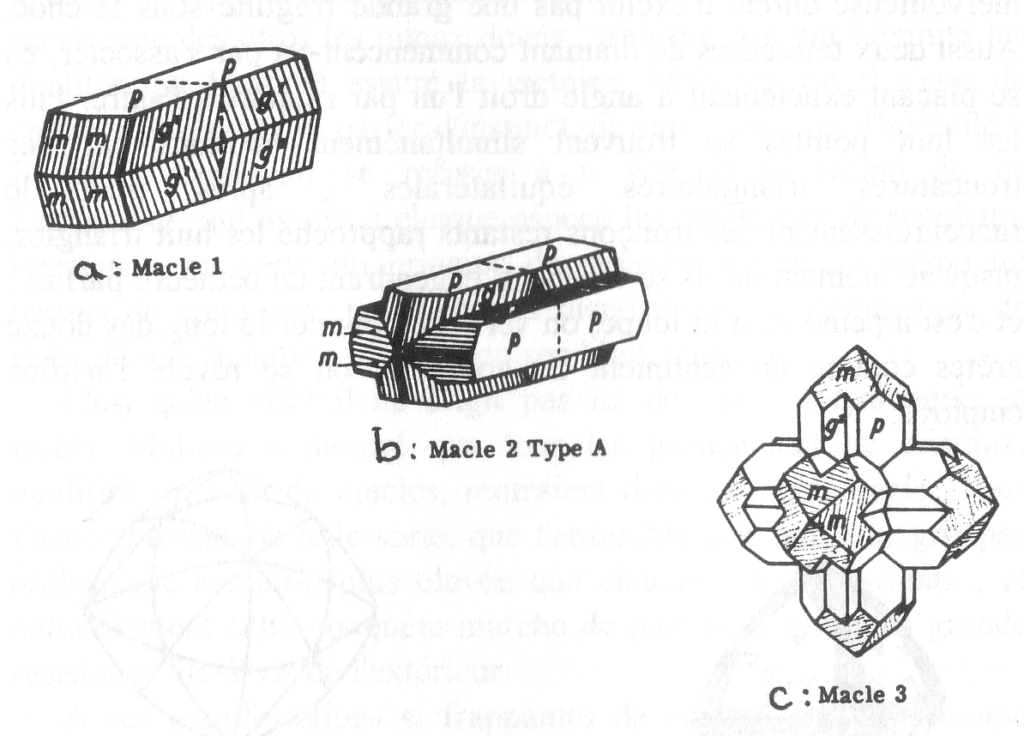
Fig. 3. Christianite. a) macle simple, b) en croix grecque, c) croix assemblées dans les 3 directions.

Mais ce n’est pas assez. Dans un solide, tout angle rentrant est une cause de faiblesse, en multipliant les surfaces d’attaques. Or, de ces angles rentrants, la christianite renferme visiblement trop. Alors on la voit se ramasser en quelque sorte sur elle-même, en contractant ses trois colonnes vers leur rencontre commune. Enfin un moment vient où les six pyramides terminales⁵, amenées au contact, se soudent exactement les unes aux autres, transformant l’assemblage en un solide régulier à douze faces, de tous les polyèdres cristallins celui qui présente, sans cesser d’avoir des faces planes, la forme la mieux rassemblée, la plus voisine d’une sphère.

Un art égal se trouve déployé dans l’assemblage de deux cristaux de diamant. Individuellement, par sa symétrie, le diamant n’a droit qu’à la forme de la pyramide à quatre faces, dite tétraèdre régulier.

Mais cette pyramide a des arêtes bien saillantes et des angles bien pointus, danger sérieux pour une substance dont la merveilleuse dureté n’exclut pas une grande fragilité sous le choc. Aussi deux tétraèdres de diamant commencent-ils par s’associer, en se plaçant exactement à angle droit l’un par rapport à l’autre. Puis les huit pointes se trouvent simultanément abattues par des troncatures triangulaires équilatérales ; après quoi le raccourcissement des tronçons restants rapproche les huit triangles, jusqu’au moment où ils se touchent, engendrant un octaèdre parfait ; et c’est à peine si, à la loupe, on verra se dessiner le long des douze arêtes comme un sentiment de gouttière, où se révèle l’artifice employé.

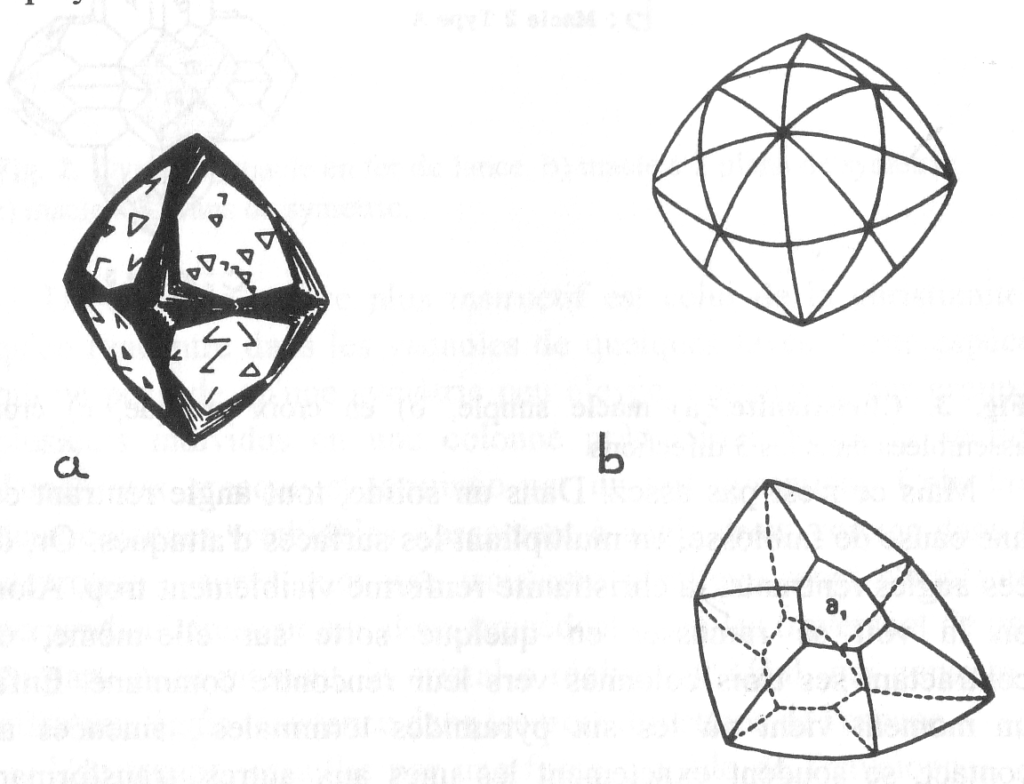
Fig. 4. Diamant. a) macle commune, b) massif (courbe).

Ce n’est pas tout ; il arrive souvent que les faces de la pyramide octaédrique se chargent d’une série de facettes en escalier, dont les contours se fondent les uns dans les autres.

Ainsi le cristal devient courbe et ne présente plus aucun élément sur lequel puissent mordre les agents usuels de destruction.

Si des combinaisons aussi savantes, au lieu d’être réalisées dans le monde minéral, se rencontraient, comme les faits de mimétisme, parmi les individus du règne organique, il se trouverait sans doute quelque disciple de Darwin pour en trouver la raison dans la loi de survivance des êtres les mieux doués , transmettant par hérédité les qualités qui leur ont assuré la victoire. Mais ici, où il s’agit de cristaux, qui pourrait parler d’instinct, de survivance ou d’hérédité ? Et alors, comment se refuser à y voir l’intervention de ce Législateur, qui assure à chaque espèce les conditions de meilleure résistance, en vertu du principe de moindre action, et même lui permet de conquérir, par d’habiles dispositions, beaucoup plus de stabilité que sa nature propre n’en semblait comporter !

C’est qu’en effet il ne s’agit pas ici de faits exceptionnels et isolés. Mallard a montré que tous les groupement de cristaux, qualifiés du nom de macles, rentraient dans la même règle. Tous s’accomplissent de telle sorte, que l’ensemble des individus groupés réalise une symétrie plus élevée que chacun des composants ; et naturellement cette conquête marche de pair avec une plus grande résistance vis-à-vis de l’extérieur.

A ces manifestations si frappantes de l’ordre et de l’harmonie s’ajoute un autre enseignement, qu’il nous paraît bon de recueillir en passant.

Par une dérogation fréquente à la loi chimique des proportions définies, l’expérience nous apprend que deux corps différents peuvent, dans certains cas, cristalliser ensemble en toutes proportions. C’est la propriété que les chimistes désignent sous le nom d’isomorphisme, et qui se manifeste quand les corps ainsi susceptibles de s’associer ont des compositions chimiques semblables et des formes individuelles très voisines ; tels sont les sulfates de fer, de magnésium et de zinc ; tels aussi les carbonates de calcium, de magnésium, de manganèse et de fer, etc., etc. , Ainsi se forment des cristaux très nets, mais de composition complexe.

Il en est, comme les sulfates précités, qu’on peut produire à volonté dans les laboratoires, en vérifiant que, pour une quantité invariable d’acide sulfurique, il est loisible de faire intervenir les proportions respectives qu’on veut des oxydes de fer, de zinc et de magnésium, sans que cela trouble en rien la limpidité ni la netteté des cristaux, dont les angles seuls présentent une très légère variation, en rapport avec la nature du composants qui prédomine.

L’explication de l’isomorphisme paraît extrêmement simple : deux particules non identiques sont néanmoins admises dans le même édifice, parce qu’elles diffèrent assez peu pour que leur coexistence ne trouble pas la symétrie générale. Cet arrangement met donc en évidence ce que nous nous permettrons d’appeler la tolérance de la nature. Un architecte intransigeant, ayant résolu d’exécuter une construction avec des cubes de pierre, les refuserait impitoyablement sur le chantier si, à la vérification, il ne trouvait pas toutes les arêtes rigoureusement égales, ni tous les angles exactement droits. Au lieu de cela, un constructeur plus tolérant se contentera de demander que les différences ne dépassent pas une certaine limite ; et alors, par d’heureuses combinaisons de ces cubes un peu défectueux, en corrigeant les inégalités des uns par les défauts en sens contraire des autres, il saura donner à sa construction un aspect d’ensemble assez correct pour que nul n’y trouve à redire.

Ainsi, oserions-nous conclure, a procédé le Souverain Architecte. Par là, il nous a donné une leçon dont il y aurait profit à nous inspirer, même dans d’autres domaines que celui de l’architecture. Si ce n’est pas tout à fait employer le minimum d’efforts, ce serait du moins manifester le minimum d’exigences, et éviter entre les hommes le plus possible de frottements. D’ailleurs, puisque le frottement ne peut être vaincu que par un travail mécanique, en prenant soin de le diminuer, on se montrerait encore fidèle à la règle de la moindre action.

______________

(N.B. Les figures nécessaire à l’intelligence de cet article ont été extraites du recueil établi par Raymond Fischesser, « Données des principales espèces minérales », Paris, Sennac, 1955.)

---

1 Extrait de « Science et Apologétique« , Paris, Bloud 1905, pp.140-157.

2 Fondateur de la chaire de géologie à l’Institut Catholique de Paris, Albert de Lapparent (1839-1908) était membre de l’Académie des Sciences.

3 H. Poincaré, La Science et l’hypothèse, Paris, Flammarion,p.154.

4 Dédiée au roi Christian VIII du Danemark par des Cloizeaux (1847).

5 En grisé sur la figure.